Поиск пути
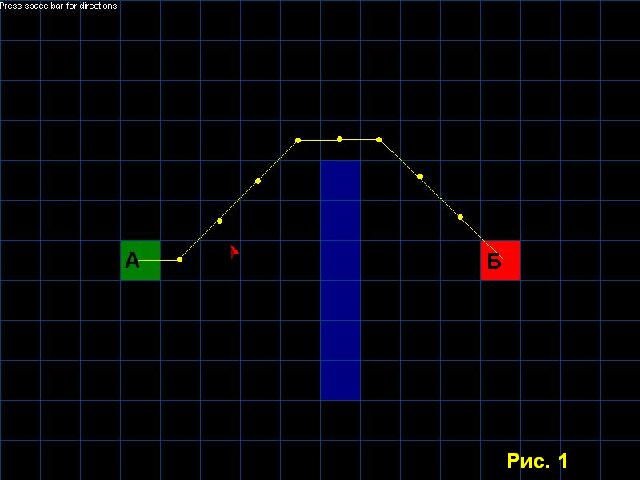
Каждый программист, когда-нибудь задумывается, а как сделать, чтобы монстры тупо не бились в стенку, а умели обходить ее, при этом по самому быстрому пути. Для этого существует целый ряд алгоритмов, но я вам расскажу только об одном, о самом распространенном А*(а стар). Суть этого алгоритма заключается в следующем: рис.1 есть точка А и точка Б, нужно добраться из т. А до т. Б. Самый быстрый путь указан стрелочками. Так разберемся поподробнее. Поле разбито на квадраты. Квадрат должен быть размером с самый маленький объект, который может представлять из себя препятствие. Центр квадрата принято называть вершиной. У каждого перемещения ест цена, т.е. прямо идти быстрее чем по диагонали. Цена если идти прямо будет 10, а если по диагонали то 14(1.414 корень из 2).
Ну что ж давайте перейдем к практике. Поиск пути начинается перебором соседних клеток А, перебор идет до тех пор пока не достигнет конечной цели. Все соседние клетки в данный момент находятся в открытом списке(в открытый список заносятся точки которые необходимо проверить). Далее мы выбираем одну из соседних клеток и производим следующее:
1. Проверяем граничащие клетки с родительской(с начала пути родительской клеткой является т. А), если они являются препятствием пропускаем их).
2. Добавляем родительскую клетку в закрытый список).
Оценка:
T = стоимость передвижения из стартовой точки к данной клетке
I = примерная стоимость передвижения от данной клетки до целевой.
Стоимость G вычисляется по формуле
G = T+I
T вычисляется путем прибавления к T родительской точки 10 или 14 в зависимости от по диагонали или прямо мы идем.

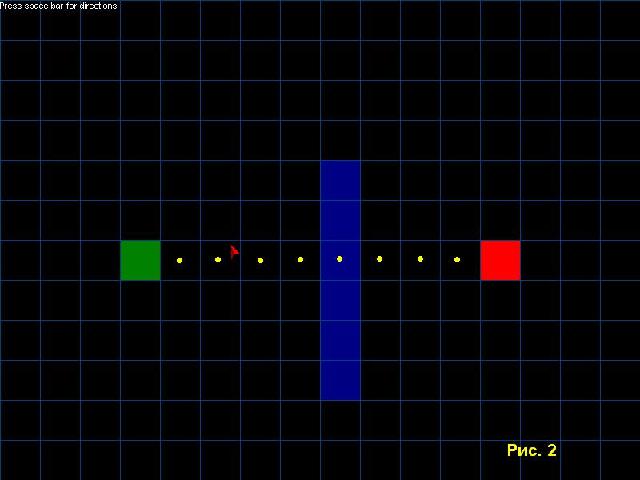
I же вычисляется путем подсчета вертикальных и горизонтальных клеток от начальной точки до конечной и это число умножается на 10. рис2.
Вот алгоритм вычисления пути:

1) Добавляем стартовую точку в открытый список
2) Проверяем следующее:
a) Ищем в открытом списке клетку с наименьшей стоимостью G
b) Помещаем ее в закрытый список и удаляем из открытого
c) Для каждой из соседних клеток(их 8)
• Если клетка не проходима или находится в закрытом списке, игнорируем ее
• Если клетка еще не в открытом списке, то добавляем ее туда
• Если клетка уже в открытом списке, то проверяем ее дешевизну(дешевил ли будет путь через эту клетку).Для используем стоимость T, более низкая стоимость T указывает на более дешевый путь. Если это так то меняем родительскую клетку на текущую и пересчитываем для нее стоимость T и G. Если вы сортируете открытый список по стоимости G, то придется перестроить весь список заново.
d) Останавливаемся если:
• Добавили в открытый список целевую клетку, т.е. путь найден
• Или открытый список пуст и целевая точка не достигнута, т.е. путь не найден.
3) Сохраняем путь. Двигаемся от целевой точки до стартовой через родительские – это и будет наш путь.

Ну, вот в принципе и все. Надеюсь, я помог вам этой статьей.